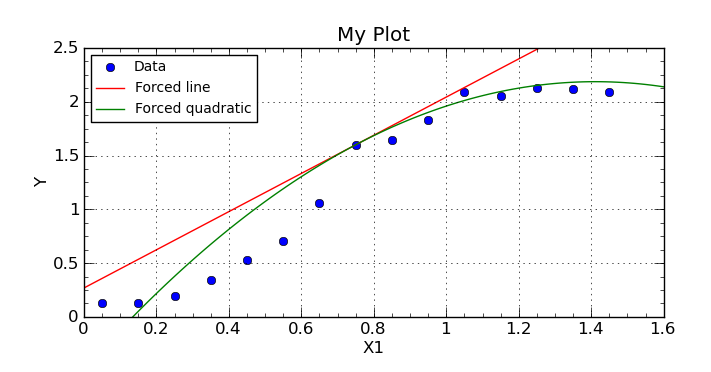
Forcing a curve fit through a specific point
If you want to force a particular curve fit through a specific point, you can do so via the advanced models in CurveExpert Pro (you can actually do it via a one-line equation as well, but the result is a little ugly). Forcing through a point acknowledges that you lose one parameter in your fit; meaning that one parameter must obey a specific relationship given the other np-1 parameters. So, just solve for the one and compute it appropriately in the model.
For example, if you want to force a line 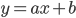 through a given point (
through a given point (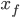 ,
,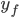 ), we have
), we have 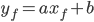 , so upon rearranging,
, so upon rearranging, 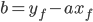 . There is only one free parameter left out of the two, which is
. There is only one free parameter left out of the two, which is 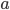 . Implementing this condition in an advanced user model looks like this (some comments removed for brevity):
. Implementing this condition in an advanced user model looks like this (some comments removed for brevity):
[python]
name = "Forced line"
equation = "a*x + b"
latexequation = r"a x + \tilde b"
nindvar = 1
def evaluate(x,a):
xf = 0.75
yf = 1.6
btilde = yf - a*xf
return a*x + btilde
def initialize(x,y):
return 1.0,
[/python]
Doing the same thing with a quadratic, we have 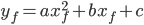 , so upon rearranging,
, so upon rearranging, 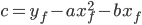 . Thus, we only have two free parameters
. Thus, we only have two free parameters 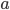 and
and 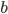 . Implementing this condition in an advanced user model looks like this:
. Implementing this condition in an advanced user model looks like this:
name = "Forced quadratic"
equation = "a*x^2 + b*x + c"
latexequation = r"a x^2 + bx + \tilde c"
nindvar = 1def evaluate(x,a,b):
xf = 0.75
yf = 1.6
ctilde = yf - xf*(a*xf + b)
return x*(a*x + b) + ctildedef initialize(x,y):
return 1.0,1.0
[/python]
We can see the results of the two curve fits below. The optimizer has chosen the best (free) coefficients possible to fit the data, under the constraint that the curve must pass through the point (0.75,1.6).